MobileNetV1에 대한 간단한 논문 리뷰입니다.
논문링크 : https://arxiv.org/abs/1704.04861
Abstract
해당 논문에서는 Mobile 기기와 임베디드 비전 어플리케이션을 위한 효율적인(efficient) 모델인 MobileNets를 소개합니다. MobileNet은 depth-wise convolutions를 이용하여 모델의 아키텍쳐를 구성하였으며 간단한 2개의 하이퍼파라미터를 이용하여 지연시간(latency)과 정확도(accuracy)를 절충합니다.
1. Introduction
더 높은 accuracy를 달성하기 위해 Convolutional neural networks는 더 깊고, 복잡해지는게 트렌드였습니다. 하지만 로보틱스, 자율주행 자동차, AR, 사물인식과도 같은 테스크의 실생활의 어플리케이션들은 계산적(computationally)으로 제한된 플랫폼에서 빠르게 수행되어야 합니다.

2. Prior Work
MobileNet 이전의 모델을 가볍게 하는 방법들이 나와있습니다.
3. MobileNet Architecture
MobileNet의 아키텍쳐는 depth-wise Seperable convolutions로 구성됩니다. 그리고 도움을 주는 2개의 하이퍼파라미터에 대해서도 이야기할 것 입니다.
3.1. Depthwise Separable Convolution
Depthwise Seperable Convolution을 보기 전에 우리 모두에게 익숙한 standard convolution 연산을 먼저 봅시다.

CNN이란 위의 gif 처럼 아웃풋(convolved feature)이 나오기 위해서 커널이 인풋 이미지(Image)를 convolving 하면서 만들어집니다.

DF x M은 width x height x channel의 크기인 인풋이 됩니다. 그리고 Dk x Dk x M의 사이즈인 N개의 커널을 이용하여 오른쪽의 아웃풋을 만들게 됩니다. 따라서 계산해야하는 연산량은 아래와 같습니다.

한 개의 커널이 인풋에서 한 번 연산할 때의 연산량은 $D_k^2$ x $M$이 됩니다. 그리고 위에서 본 convolution gif 처럼 한 개의 커널이 인풋 하나를 처리하기 위해 $D_G^2$ 번 연산 해야하기 때문에 총 필요한 연산은 $D_G^2$ x $D_k^2$ x $M$이 될 것 입니다. 그리고 한 개의 커널이 아닌 총 N개의 커널이 있다면 아웃풋은 $N$ x $D_G^2$ x $D_k^2$ x $M$이 될 것입니다.
이제 depthwise seperable convolution이 기존의 CNN 연산량인 $N$ x $D_G^2$ x $D_k^2$ x $M$ 보다 어떻게 줄이는지 한 번 봅시다. Depthwise seperable convolution은 아래와 같이 총 두 단계로 나누어져 있습니다.
- Depthwise convolution: Filtering stage, 인풋 --> $D_G$ x $D_G$ x $M$
- Pointwise convolution: Combination stage, $D_G$ x $D_G$ x $M$ --> $D_G$ x $D_G$ x $N$
1. Depthwise convolution: Filtering stage
위에서 이야기했던 우리가 익숙한 standard convolution 연산에서는 한 개의 커널이 채널 M에 대해서 연산을 했습니다. 하지만 이번엔 다르게 커널의 채널이 1인 커널로 인풋에 대해 1채널에 대해서만 연산을 합니다. 커널의 모양이 $D_k$ x $D_k$ x 1 입니다.

이제 연산량을 계산해보겠습니다. 한 개의 커널이 인풋에 대해 한 번 연산할 때는 $D_k^2$ 입니다. 그리고 1 채널에 대해 연산을 하려면 $D_G^2$ x $D_k^2$ 이 필요합니다. 그리고 총 M개의 커널이 있기 때문에 Depthwise Convolution의 총 연산량은 $M$ x $D_G^2$ x $D_k^2$ 이 됩니다.

2. Pointwise convolution: Combination stage
이번에는 커널의 모양이 1 x 1 x M입니다. 아웃풋은 우리가 위에서 이야기한 standard convolution의 아웃풋과 같습니다. 같은 아웃풋으로 과연 얼마의 연산량이 차이날지 Pointwise convolution 연산량 을 계산한 후 총 연산량을 살펴봅시다.
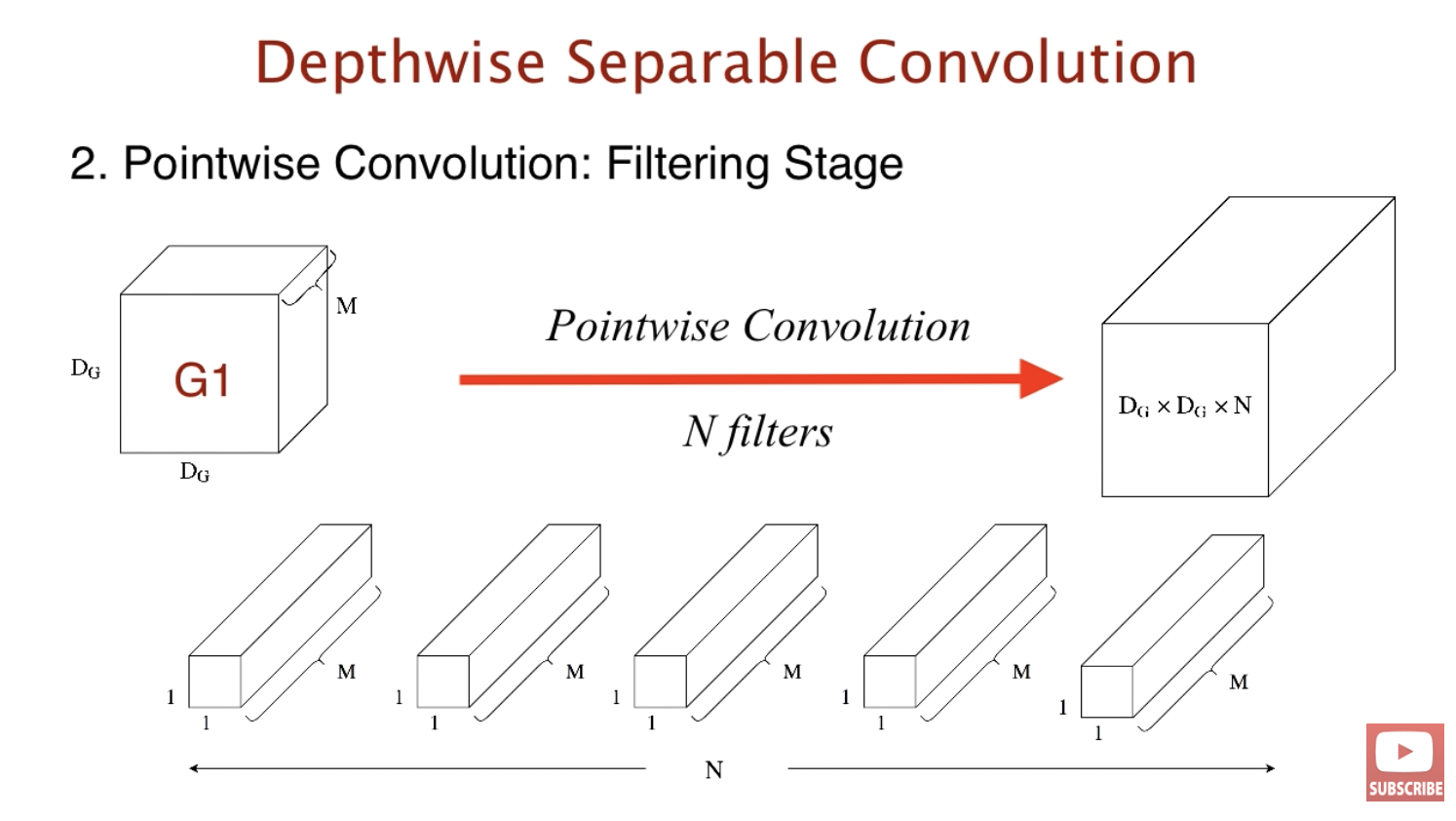
1개의 커널이 인풋에 대해 계산하기 위해서는 $D_G$ x $D_G$ x $M$ 이 필요합니다. 따라서 pointwise convolution의 총 연산량은 $N$ x $D_G^2$ x $M$와 같습니다.
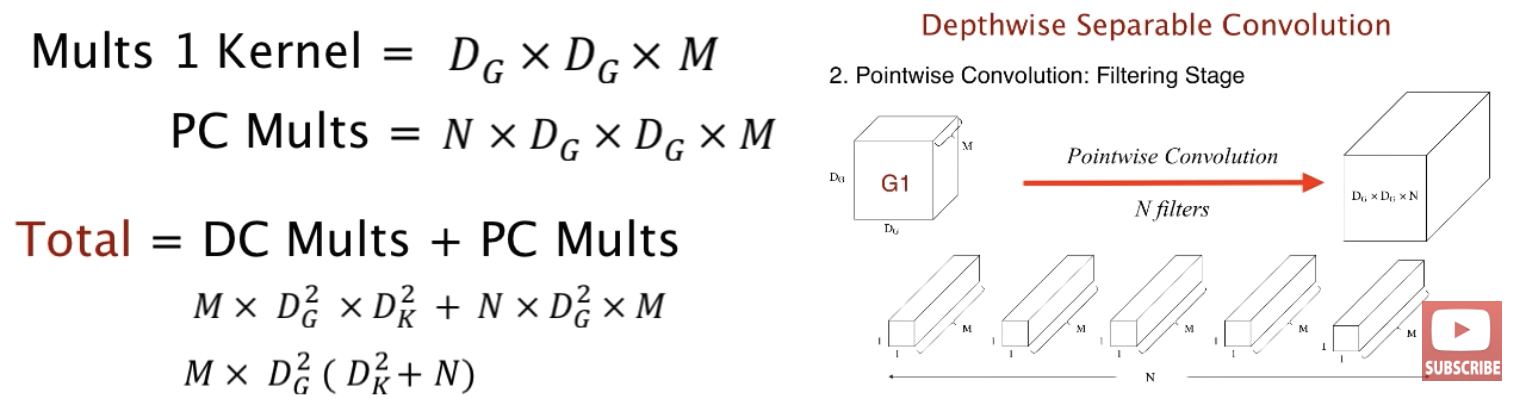
따라서 depthwise sperable convolution의 총 연산량(DC Mults + PC Mults)는 $M$ x $D_G^2$ x $D_k^2$ + $N$ x $D_G^2$ x $D_G^2$ x $M$와 같고 standard convolution에 비해 얼마나 줄었는지 살펴보겠습니다.

비율을 계산해보면 약 1/9배 정도의 연산량으로 줄어들었습니다.

이렇게 연산량이 줄어드는 Depthwise Separable Convolution를 아키텍쳐로 적용했습니다.
3.2. Network Structure and Training

위의 figure 3과 같이 MobileNet은 기존의 standard convolution과 비교하여 다른 방법으로 레이어를 쌓았습니다.
3.3. Width Multiplier: Thinner Models
Width multiplier의 역할은 각 레이어에서 네트워크를 균일하고 작게 만드는 것입니다.
논문에서는 α로 표현하고 있고, 인풋과 아웃풋의 채널에 곱하여 사용합니다. 채널의 크기가 M일 때 αM으로 표현합니다. α ∈ (0, 1] 의 수이며 논문에서는 1, 0.75, 0.5, 0.25와 같이 특정한 수로 세팅하였습니다. α = 1일 때 baseline MobileNet 이라고 하며 α < 1 일 때 reduced MobileNets 이라고 합니다.
3.4. Resolution Multiplier: Reduced Representation
Resolution Multiplier의 역할은 네트워크의 computational cost를 줄이는 것입니다.
두 번째 하이퍼파라미터인 resolution multiplier는 인풋의 width, height에 곱하여 사용합니다. 기호는 ρ로 표현합니다. ρ ∈ (0, 1] 의 수이며 논문에서는 인풋 사이즈가 224, 192, 160 or 128 였습니다. ρ = 1 일 때 baseline MobileNet 이라고 하며 ρ < 1 일 때 reduced computation MobileNets 이라고 합니다.
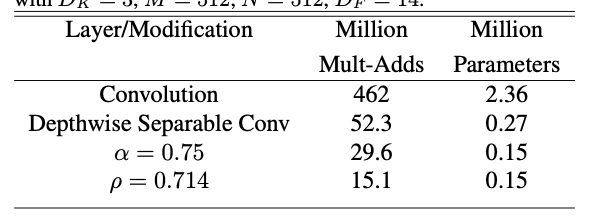
Depthwise Spearable Conv와 Width multiplier, Resolution Multiplier를 적용했을 때 확실히 백만 단위곱과 파라미터 개수가 줄어든 것을 볼 수 있습니다.
4. Experiments
이 섹션에서는 단위곱과 파라미터가 줄어든 상황에서 어느정도의 정확도를 보이는지 실험을 보여줍니다.
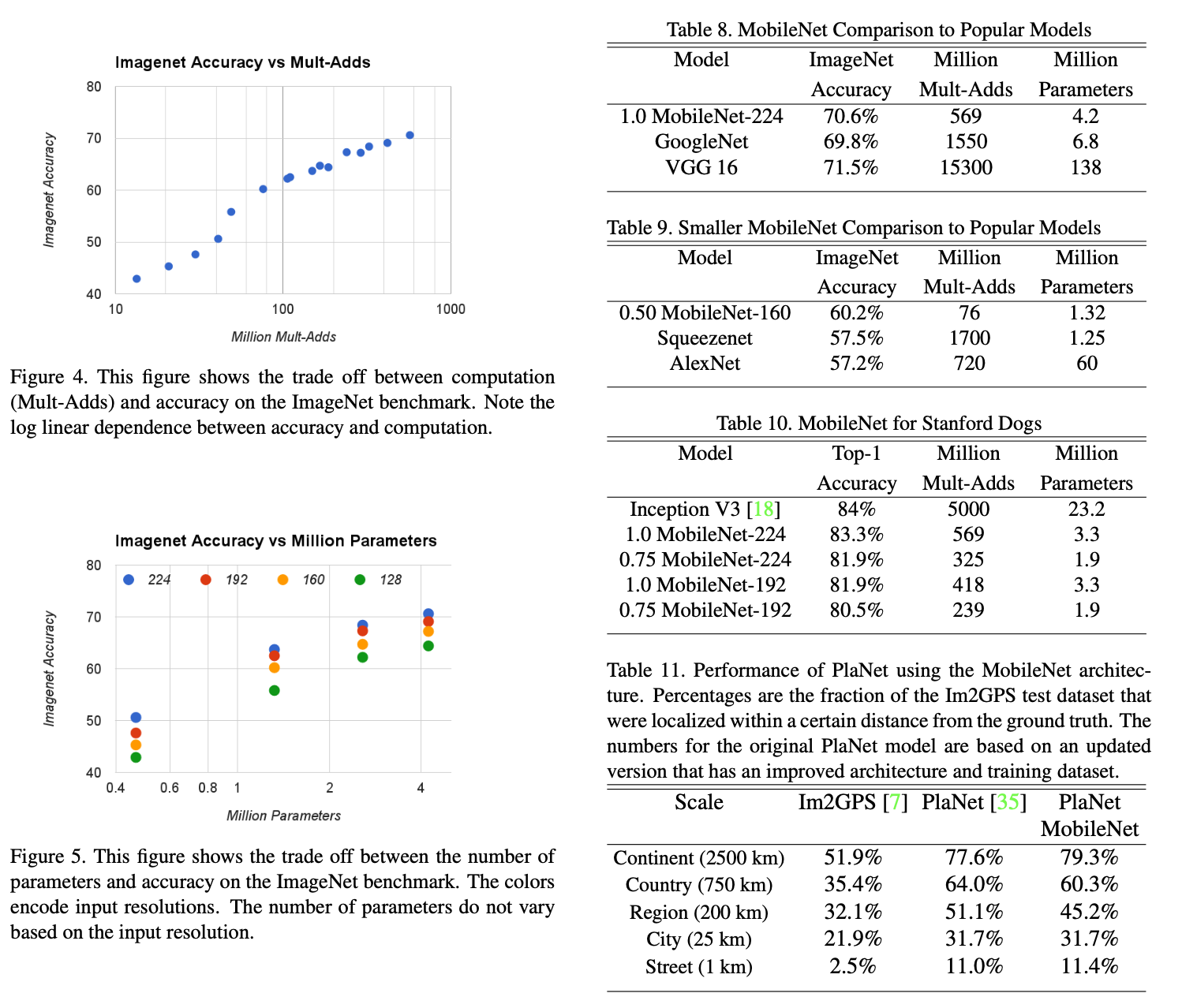
Table 들을 보면 더 적은 양의 단위곱과 파라미터 개수로도 ImageNet으로 테스트했을 때 비슷한 accuracy를 얻어낼 수 있다는 것을 보여줍니다. 다양한 테스크에 대한 실험들을 보여줍니다.
참고
'DL|ML' 카테고리의 다른 글
| <혼자 또는 같이하는 머신러닝 스터디 잼> 티셔츠 대장정의 끝 (0) | 2021.05.20 |
|---|---|
| 정확히 CNN에서 shared weights란 무엇을 의미하나요? (0) | 2021.05.12 |
| <혼자 또는 같이하는 머신러닝 스터디 잼> Intro to Deep Learning 코스 요약 (2) (0) | 2021.04.16 |
| <혼자 또는 같이하는 머신러닝 스터디 잼> Intro to Deep Learning 코스 요약 (1) (0) | 2021.04.16 |
| <혼자 또는 같이하는 머신러닝 스터디 잼> Intermediate Machine Learning 코스 요약 (1) | 2021.04.07 |



